Python機械学習アルゴリズム学習備忘録。今回は強化学習 – Upper Confidence Bound (UCB) – について。
内容は、Udemy 
の「【世界で74万人が受講】基礎から理解し、Pythonで実装！機械学習26のアルゴリズムを理論と実践を通じてマスターしよう」で学んだ内容を自分用備忘録としてまとめたものです。
参考：みんなのAI講座 ゼロからPythonで学ぶ人工知能と機械学習
強化学習とは
まず、強化学習とはなにか。
強化学習とは、機械の学習過程で、報酬（や罰則）を与え、機械が報酬を最大化するように学習していくアルゴリズムのこと。
例えば、犬におすわりを覚えさせるとき。「おすわり」と言ってちゃんとおすわりをした場合は、エサ（＝報酬）を与え、ちゃんとおすわりできなかったときは何も与えない、とする。
何度も繰り返しているうちに、犬はだんだんと「どのような行動を取れば報酬がもらえるか」を学習し、自分が得られる報酬が最大化するようになる。（＝おすわりができるようになる。）
多腕バンディット問題 (Multi Armed Bandit)
次に、多腕バンディット問題というものを考える。
これは一般的には複数台あるスロットマシンを例として考えるが、その前に直感的に理解するために、ある人がラーメン屋にラーメンを食べに行く、という状況を例に考える。
その人の家の近所にラーメン屋が５軒あるとする。そのうち行ったことのあるラーメン屋は１軒だけ。その既知のラーメン屋の満足度を１０段階のうち７点とする。
このとき、その人にはラーメン屋を選ぶ方法として「活用」と「探索」という選択肢がある。
まず、既知のラーメン屋に行く場合、その人は、その既知のラーメン屋に関してすでに持っている情報を「活用」していることになる。
次に、まだ行ったことのない残りの４軒のラーメン屋に行く場合、その人は「探索」を行っているといえる。
このとき、５軒のラーメン屋の実際の満足度が以下の通りだとする。（A以外のラーメン屋の満足度は行くまでわからない。）
| A | B | C | D | E |
| 7 | 5 | 8 | 9 | 4 |
このとき、既知のラーメン屋Aにだけ行き続けた場合、満足度は次のようになる。
次に、A以外のラーメン屋にもランダムに探索を行った場合、満足度は次のようになり得る。
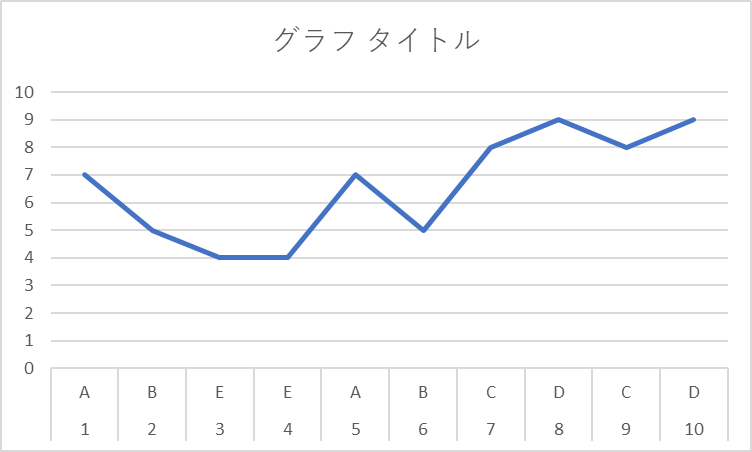
このように訪問回数が多い場合でみると、より満足度の高いラーメン屋を見つけた段階で、その満足度の高いラーメン屋に行く頻度が多くなっていく。
一方で、訪問回数が少ない段階では、満足度の低いラーメン屋に当たる可能性もあり、既知のラーメン屋の情報を活用するほうが満足度（＝報酬）が高くなる。
Upper Confidence Bound (UCB)
これを５台のスロットマシンに置き換えて考え、Upper Confidence Bound(以下、UCB)について考える。
５台のスロットマシンに関する事前情報はまったくないものとすると、５台それぞれに対する期待値はすべて同じ。
| A | B | C | D | E |
| 5 | 5 | 5 | 5 | 5 |
一方で、各マシンの本来の期待値が以下の通りだとする。
| A | B | C | D | E |
| 5 | 4 | 2 | 6 | 3 |
スロットをやり始めた時点では、結果の予測に対する信頼度は５台とも同じ。
このとき、信頼度を、同じ幅を持つ棒グラフのようなものと考える。
試行回数を増やすと、結果が蓄積されるので、各スロットマシンの結果に対する予測の信頼度が増す。予測の信頼度が増えたとき、信頼度の棒グラフを縮小させる。
一方で、いい結果が出ると予測し、本当にいい結果が出た場合は、信頼度の棒グラフに+1上乗せして棒グラフの幅を拡大する。
これを繰り返していくと、５本の棒グラフの幅は、それぞれのスロットマシンが持つ本来の期待値どうしのバランスに収束していく。
つまり、はじめは、全く同じ信頼度で、
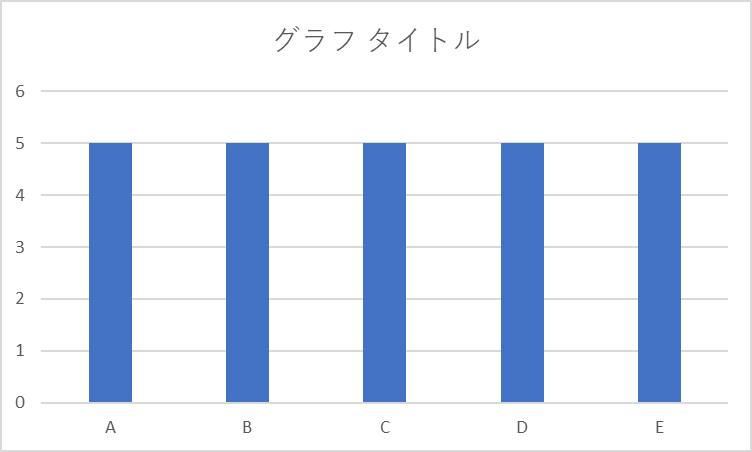
こうだったものが、試行を繰り返すうちに、
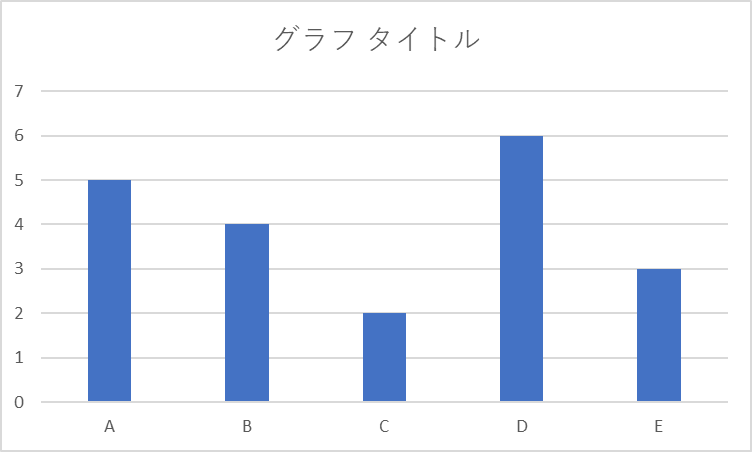
このような形に収束していく。
このとき、棒グラフの一番上の端の位置(=Upper Confidence Bound)が、最も高い位置にあるスロットマシンが、報酬を最大化する台である、と判断されるようになる。
数式でみるUpper Confidence Bound (UCB)
ここまで書いてきたUCBのアルゴリズムを数式で表すと次のようになる。
Step 1. それぞれのラウンドnにおいて、広告iに対して以下の数字を求める
Ni(n) : ラウンドnまでに、広告iが選ばれた回数
Ri(n) : ラウンドnまでの、広告iの累積報酬
Step 2. 上記の２つの数字において、以下を計算
ラウンドnまでの、広告iからの平均報酬：r’i(n) = Ri(n) ÷ Ni(n)
ラウンドnにおける信頼区間(r’i(n) – Δi(n), r’i(n) + Δi(n))
Δi(n) = √3/2 x √log(n)/Ni(n) ⇛Δi(n)の値は、Ni(n)が大きくなるほど小さくなる。逆に試行回数nが大きくなるほど、log(n)の値は大きくなり、Δi(n)の値も大きくなる。
Step 3. UCBが最大となる広告iを選ぶ
⇛r’i(n) + Δi(n)
Pythonによる実装１ -ライブラリのインポート-
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import mathPythonによる実装２ – データセットのインポート –
dataset = pd.read_csv('ファイル名.csv')
Pythonによる実装３ – UCBの実装 –
N = 10000 # データセットの行の数。つまり、ラウンドの数。いきなりすべてのラウンドをやってもいいし、この値を変えながら、信頼区間の変化を追ってもいい
d = 10 # 対象データの数。例えば、１０個の広告があるとすると、d = 10となる。
ads_selected = [] # アルゴリズムで選択した平均報酬+信頼区間の値が高い広告の番号を入れるリスト。
numbers_of_selections = [0] * 10 # １０個ある広告のそれぞれが選ばれた回数を入れるリスト。最初は0で都度更新していく。
sums_of_rewards = [0] * 10 # 広告ごとの報酬の合計値を格納するリスト
total_rewards = 0 # 評価指標の一つとして。sums_of_rewardsを全部足したもの。全体で何回報酬を得たのか確認するための変数。
for n in range(0, N):
max_upper_bound = 0
ad = 0
for i in range(0, d):
if (numbers_of_selections[i] > 0): # 一番最初の段階では、numbers_of_selectionsがすべて0なので、後の処理で、0で割る、というエラーが起こらないように条件分岐させる。
average_reward = sums_of_rewards[i] / numbers_of_selections[i] # 平均報酬
delta_i = math.sqrt(3/2*math.log(n + 1) / numbers_of_selections[i])
upper_bound = average_reward + delta_i
else:
upper_bound = 100000000 # upper_boundの値を適当に大きな値にして、すべての広告が最低１回以上選ばれるように処理を作っていく
if upper_bound > max_upper_bound: # 算出されたupper_boundがそれまでのmax_upper_boundよりも大きい場合、max_upper_boundの値を更新する
max_upper_bound = upper_bound
ad = i
ads_selected.append(ad) # 選ばれた広告の番号を格納
numbers_of_selections[ad] = numbers_of_selections[ad] + 1 # 選ばれた広告番号の選ばれた回数を更新
reward = dataset.values[n, ad] # 実際にユーザーがその広告をクリックしている場合、データセットに入っている、広告がクリックされたときの値（=1)を報酬として格納する。広告が実際にはクリックされていなければ、0が入る。
sums_of_rewards[ad] = sums_of_rewards[ad] + reward
total_rewards = total_rewards + reward
numbers_of_selections
Pythonによる実装4 – 結果の可視化 –
# ヒストグラムでそれぞれの広告がアルゴリズムによって選ばれた回数の合計を表示している。
plt.hist(ads_selected)
plt.title('Histogram of ads selections')
plt.xlabel('Ads')
plt.ylabel('Number of times each ad was selected')
plt.show()その他・参考
強化学習入門：多腕バンディット問題多腕バンディット入門：3つのアルゴリズムをpythonで実装する
【機械学習アルゴリズム学習備忘録】強化学習 – Thompson Sampling-
コメント