Python機械学習アルゴリズム学習備忘録。ディープラーニングについて。今回は畳み込みニューラルネットワーク編です。
内容は、Udemy の「【世界で74万人が受講】基礎から理解し、Pythonで実装!機械学習26のアルゴリズムを理論と実践を通じてマスターしよう」で学んだ内容を自分用備忘録としてまとめたものです。
前回までの記事で基本的なディープラーニングの考え方と実装について書いたので、今回は畳み込みニューラルネットワークについての備忘録を書いていきます。
参考
みんなのAI講座 ゼロからPythonで学ぶ人工知能と機械学習
【機械学習アルゴリズム学習備忘録】ディープラーニング その1 – 基礎編 –
【機械学習アルゴリズム学習備忘録】ディープラーニング その2 – 実装編 –
畳み込みのイメージ
まずは、畳み込みのイメージから。
ある画像があるとして、その画像を特定のフィルターを通して、いくつかのブロックごとに数値データに置き換えていく。例えば、白い部分は0、黒い部分は1のように。
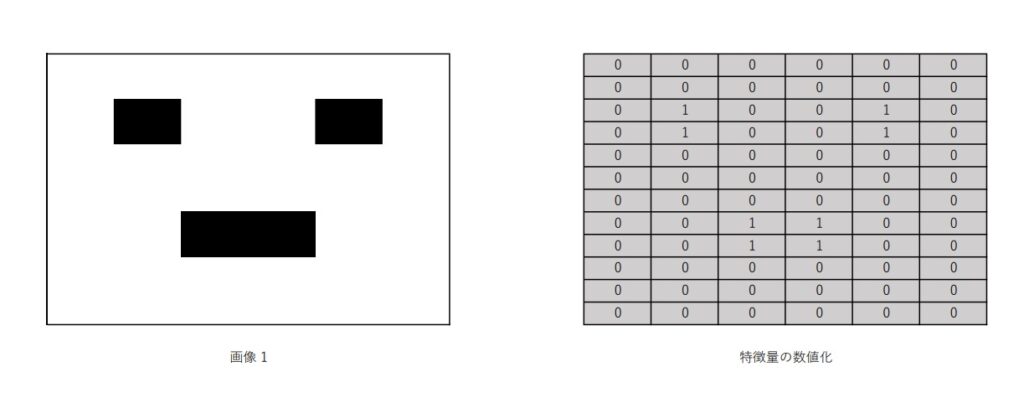
次に、その格子状データに対して、Feature Detectorというフィルターを掛けてさらに特徴量の抽出を行う。
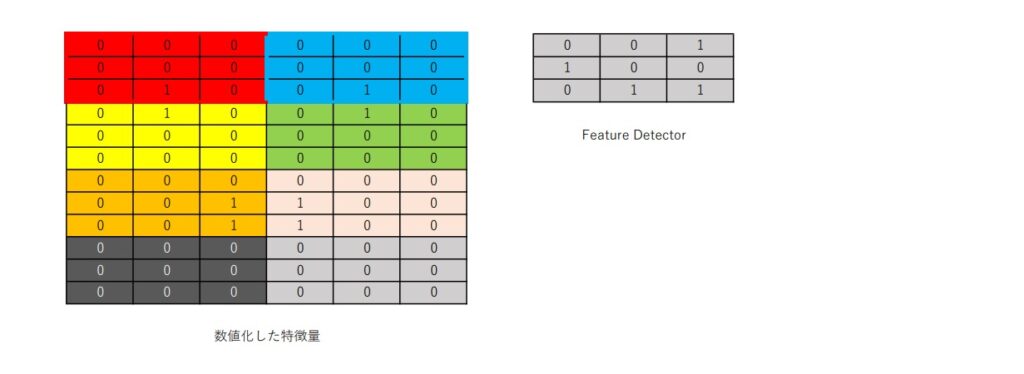
この図の左側は、先程数値化した格子状データを3 x 3のブロックごとにわかりやすいように色付けしたもの。
その右側にあるのが、Feature Detector。今回は3 x 3にしたが、必ずしも3 x 3でないといけないわけではない。抽出したい特徴や問題に応じて変えていく。
また、Feature Detectorにも抽出したい特徴や問題に応じて値が入っている。
このFeature Detectorを、各ブロックに対して掛けていく。
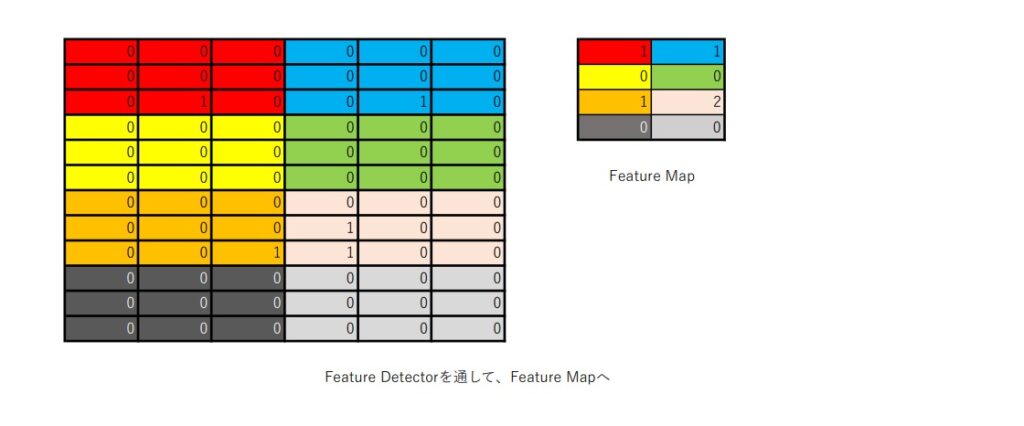
例えば、赤いブロックにFeature Detectorをかけると、赤いブロックの一番左上は、0 x 0 = 0となる。
これを全ブロックで繰り返していくと、上図の左側の図のような値になる。
今回は、ブロックごとに重ならないようにFeature Detectorを掛けていったが、例えば、一番左上のブロックにかけたあと、2マス分だけ右にスライドさせてFeature Detectorをかける、みたいな手法も問題によってはある。
そして、Feature Detectorを掛けたら、最後に各ブロックごとに値を足し合わせて、各ブロックごとの合計値を、Feature Mapに分布していく。
これで、最初の画像1の特徴量が抽出された。
これが基本的な畳み込みの考え方であり、実際の畳み込みニューラルネットワークの処理の中では、何重にもフィルター(=Feature Detector)を掛け、それを重ね合わせていくことで、より高い精度での特徴抽出ができるようになっている。
目次に戻るRelu(非線形活性化関数)を使う理由
今回の畳み込みニューラルネットワークの実装ではReluという非線形の活性化関数を使っていく。
入力→隠れ層→出力
という構造を考えたときに、入力としてデータXを入れる。そのXに重みwとバイアスaを加えたyを隠れ層で活性化関数に入れ、その演算結果をy’とする。
このy’に重みw’とバイアスa’を加えた値zを出力層に入れ、最終的に結果を出力する。
隠れ層に入力される値yは、次の式で表される。
y = wX + b (w : 重み、b : バイアス)
次に隠れ層での演算結果y’とyの値が同じである場合を想定する。
つまり、
y'(w) = y
となり、y’ = yとなる。
また、隠れ層から出力層への入力zは、次の式で表される。
z = y’w’ + b’ (w’ : 重み、 b’ : バイアス)
ここにy’ = yを代入すると、
z = (wX + b) x w’ + b’ = (ww’)X + bb’
となる。
このzは、値がいくつになるかは別にして、グラフ上で直線で表すことのできる数式、つまり、「線形」であると言える。
このことから、非線形の活性化関数を入れずに演算をすると、どんなに複雑に演算を重ねたとしても、常に結果は線形となり、うまく特徴が表現されない場合が出てきてしまう。
そのような状態を回避し、よりうまく特徴を表現できるように、隠れ層の演算の中で非線形活性化関数が使われている。
目次に戻るプーリング層
次は、プーリングについて。
プーリングとは、行列から特定の値(最大値や平均値)を取ることで特徴を際立たせる処理。
今回は、最大値を取るmax-poolingを考える。
max-poolingの場合、特定の範囲(例:2 x 2)の中で、最大の値を取得し、プーリング層として作る。
プーリングをすることによって、その対象が持つ特徴をより際出せることができる。
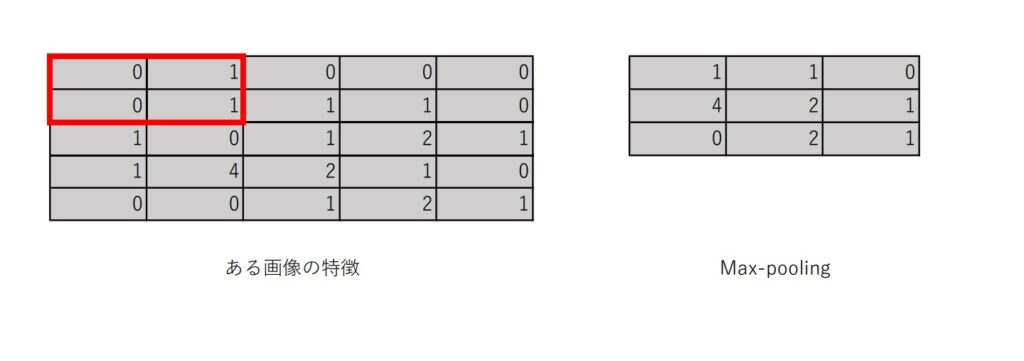
このプーリングを行うことで、例えば撮影角度の違う犬の画像が複数あっても、その犬が共通して持つ特徴を際立たせて取り出すことで、その犬の画像を判別できるようになる、といったことが可能になる。
また、精度と合わせて、プーリングによって演算処理が軽くなることも期待される。
目次に戻るFlatteningについて
Flatteningは、画像を行列データに変換したものを、さらにベクトルに変換する処理のことを指す。
目次に戻るすべての工程をつなげる
- 対象とする画像データを行列として取り込み、プーリング、Flatteningを行う。
- プーリング、Flatteningをして得たベクトルデータを入力層に入れる。
- 重みとバイアスを掛けて隠れ層に入れ、活性化関数を使って、演算処理。
- 隠れ層での演算結果に重みとバイアスを掛けたものを出力層に入れて、演算を行い、出力。誤差逆伝播法による調整を行いながらより適切な出力結果を目指していく。
softmax関数とcrossentropy (クロスエントロピー)
最後に、softmax関数とcrossentropyについてのざっくりとした直感的な理解。
例えば、ニューラルネットワークで犬か猫かの判別をするときに、ある画像が犬なのか猫なのかを確率的に判別するような場合に使われるのが、softmax関数。
crossentropyは、損失関数を求めるときに用いられる関数。
H(p,q)=−∑xp(x)log(q(x))H(p,q)=−∑xp(x)log(q(x))
回帰などのときは、最小二乗、分類のときはcrossentropyを用いるのが一般的。(絶対そう、というわけではないが比較的親和性が高いとされる。)
分類の問題の場合、ニューラルネットワークで勾配降下法を用いて誤差の調整をする際に、二乗誤差を用いると、値や場所によって勾配の大小が激しくなり、適切な調整ができない場合がある。
crossentropyの場合、対数を使っていることなどもあり、細かく調整することが可能で、そのため分類問題との親和性が高いと言われる。
交差エントロピー誤差をわかりやすく説明してみる 目次に戻る今回も少し長くなったので、実装編は、次回の記事にしようと思います。


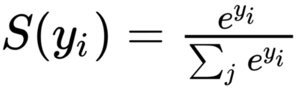


コメント