Python機械学習アルゴリズム学習備忘録。今回はディープラーニングについて。
内容は、Udemy の「【世界で74万人が受講】基礎から理解し、Pythonで実装!機械学習26のアルゴリズムを理論と実践を通じてマスターしよう」で学んだ内容を自分用備忘録としてまとめたものです。
参考:みんなのAI講座 ゼロからPythonで学ぶ人工知能と機械学習
ディープラーニングとは
そもそもディープラーニングとは何か。おなじみWikipedia先生によると。
ディープラーニング(英: Deep learning)または深層学習(しんそうがくしゅう)とは、対象の全体像から細部までの各々の粒度の概念を階層構造として関連させて学習する手法のことである[1][注釈 1]。
https://ja.wikipedia.org/wiki/%E3%83%87%E3%82%A3%E3%83%BC%E3%83%97%E3%83%A9%E3%83%BC%E3%83%8B%E3%83%B3%E3%82%B0
ディープラーニングでは、大量の入力データ(input)をもとに、機械で複雑かつ大量の演算処理を行い、分類や回帰といった問題に対する結果を出力(output)する手法のこと。
人間の脳の伝達手法(ニューロン)をイメージして作られた理論であり、人間の脳の場合、ニューロンは1千億あると言われている。

ディープラーニングは、機械学習やAIなどと合わせて最近よく耳にするようになった言葉だが、その考え方や理論自体は、1980年代にコンピューターが開発されるようになる以前からすでにあった理論である。
では、なぜ古くからある理論が最近こんなに話題になっているのか。
それは、かつてディープラーニングの理論ができたときには、コンピューターの性能が理論に追いついていなかったため、実際に理論を実現することができなかった。
しかし、近年、コンピューターの性能が急激に進化したことにより、高い演算能力を持つコンピューターが発明され、理論の実装が可能となった。
ニューラルネットワークとは
ニューラルネットワークは、ディープラーニングの手法のことで、ニューロン(人間の脳内伝播物質)を模したものである。
ニューロンは、電気信号の形で情報を受け取り(データの入力を受け取り)、情報を受け取った細胞体は、ある一定レベル以上の電気信号であれば、次のシナプスに電気信号として情報を伝達する。
この、脳内の情報伝達構造をイメージして作られたのが、ニューラルネットワークであり、ニューラルネットワークの各ノード(*)の中で行われる活性化関数を用いた演算が、情報を受け取った細胞体が次のシナプスに電気信号を伝えるかどうかを判断する仕組みと似ている。
*ノードとは、脳でいうところの情報を受け取る細胞体1つ1つがノード、というイメージで良さそう
ニューラルネットワークでは、入力されたデータをノードに伝達する際に、データに対して、重みをかけ合わせてから、ノードへ入力していく。
→この重みを掛け合わせたデータを受け取ったノードの内部で、活性化関数f(x)にデータを通して演算を行う。その演算結果を、出力層のノードに入れ、最終的に問題に対する結果を返す。
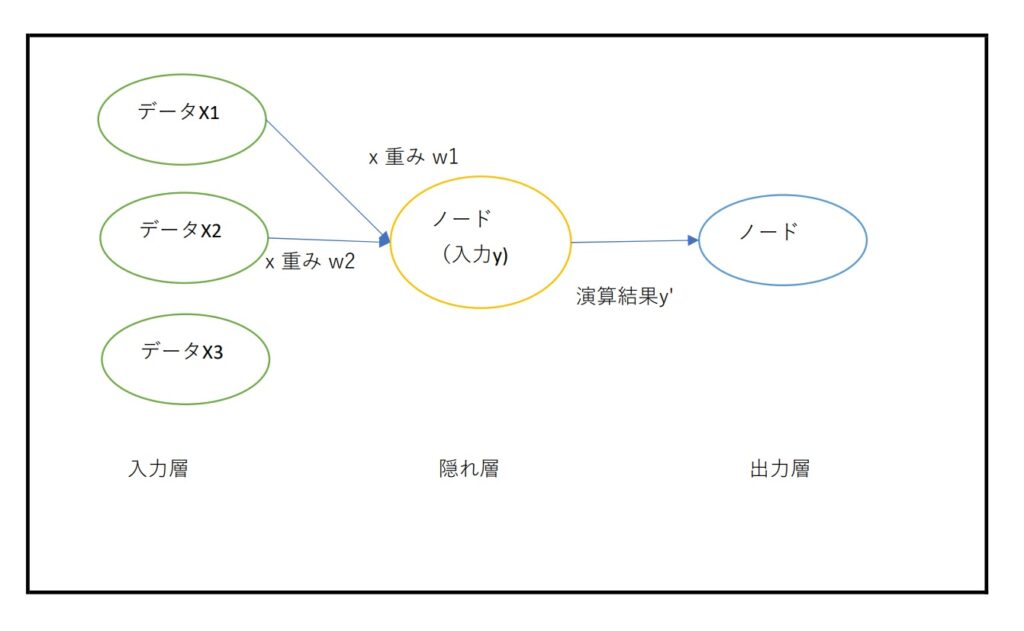
ニューラルネットワークの中では、数学的な知識が求められたり、実装したコードの中で非常に複雑な計算があったりするが、基本的な流れは上述の通り。
活性化関数の種類
上述のニューラルネットワークの流れの中の隠れ層の中で使われる活性化関数には、いくつか種類があり、問題の性質などに応じて適切なものを選択していく必要がある。
ただし、ニューラルネットワークでは非常に複雑な演算が行われているため、ある程度傾向として「こういう問題のときはこの活性化関数がよく使われる」というものはあるが、どの活性化関数を使うか、は数学的な裏付けよりも経験などが物を言うケースが多い。
活性化関数の種類(一部)
活性化関数をいくつか記載しておく。
1. ステップ関数
閾値(基本は、x = 0)で、y = 1となるような値を取る関数。
x < 0 のとき、0を出力
x > 0 のとき、1を出力
→特定の情報量のところでスパッと切りたいときに有効な関数
2. シグモイド関数
ロジスティック回帰で用いられる関数
x = 0のとき、y = 0.5となり、0 < y < 1の範囲で、xが大きくなるにつれ、ゆるやかにyが大きくなっていくように値を取る。
結果を確率的に取りたい場合に使用することができる。
3. Relu (ラング関数)
x = 0までは、y = 0
x > 0のとき、yもxの増加に合わせて増加していく。
マイナスの要素を排除し、プラスの要素のときだけ出力を返す関数。
4. ハイパボリックタンジェント
シグモイド関数に似ているが、x < 0のとき、y < 0(マイナスの値)を取る点が特徴。
上記4つ以外にもいろんな関数があるので、調べながらそれぞれの問題に適切な関数を使用していく。
<参考>
どんな風に学習していくのか
基本的な考え方は、他の機械学習と同様である。
機械学習のときは、アルゴリズムによって標準化をすべき場合とどちらでもよい場合とがある。
一方、ニューラルネットワークの場合、データの入力時に標準化をすることが一般的である。
演算が複雑になるがゆえに標準化をわざわざしなくてもいい、という考え方もあるが、逆に演算が複雑になるからこそ、標準化をすることでモデルの精度が上がりやすくなる、とも言われている。
たとえば、
モデルが算出する値:y’
正解データ: y
があるとすると、モデルが算出する値と正解データの差= y’ – yは、損失関数と呼ばれる。
→損失関数 1/2(y’ – y)^2 *y’-yの2乗 *平均二乗誤差
参考:[損失関数/評価関数]平均二乗誤差(MSE:Mean Squared Error)/RMSE(MSEの平方根)とは?
入力データに対して掛け合わせる重みwを調整していき、損失関数が0になるように演算をしていく。
例えば、シグモイド関数を活性化関数に入れた場合、シグモイド関数はxの値が大きいほどyの値が大きくなる単調増加の関数なので、重みwを大きくすればするほどyの値が大きくなる。
一方で、ニューラルネットワークの場合、一つのノードに対しての入力の重みを極大化すると、別のノードに入れるときにバランスが取れなくなることがあるので、一概に大きな重みを入れればいい、というものでもない。
すべてのノードにおいて損失関数を最小化することを目指して演算をしていく。(つまり、すべてのノードで、y’ – yが最小にするようになるようにする。)
勾配降下法
損失関数を最小化するために行われる演算手法
適当な値の重みwに対する出力値y’
損失関数 = 1/2(y’ – y)^2 (平均二乗誤差)
平均二乗誤差のグラフは二次関数のグラフになる。損失関数の二次関数グラフの「傾き」を使って、損失関数を最小化するように演算していく。
傾きがマイナスのとき(y’の値が負の値のとき)は、y’が大きくなるように調整
傾きがプラスのとき(y’の値が正のとき)は、y’が小さくなるように調整
となるように機械が自動的に演算を行っていく。
確率的勾配降下法
勾配降下法では、それぞれのデータに対しての損失の値をすべて合計したものを最小化するように重みを調整していく。
一方で、確率的勾配降下法では、データ1つずつの損失を最小化するように重みを調整していくので、勾配降下法に比べてより細かく重みを調整することができ、高い精度が期待できる。
誤差逆伝播法
適切に重みを更新していくための考え方。
モデルの出力値(y’)を変えるために出力層への入力に対する重みを変更する必要がある。
出力層への入力に対する重みを変更するということは、出力層の前のノードでの演算結果が変わる必要があり、そのためにはその出力層の前のノードへ入力する値が変わる必要がある。それはつまりさらにその前のノードから出力される値が変わる必要がある、ということになり、それを繰り返していくと結局、一番最初の入力層から演算結果の調整が必要になる。
このように出力結果を調整するために重みをどう調整するかを数式化したものが誤差逆伝播法である。
いろんな記事があるが、ややこしいので、もっと詳しく勉強したい場合は、↓のような動画で勉強するのもありかもしれない。
少し長くなってしまった気がするので、実装編は次の記事にしよう。




コメント